GRÁFICOS DO MOVIMENTO

LISTA DE EXERCÍCIOS SOBRE GRÁFICOS

Exercícios básicos

Ex 1: Um ciclista realiza um movimento uniforme e seu espaço s varia com o tempo conforme indica o gráfico. Determine o espaço inicial s₀ e a velocidade escalar v.

Ex 2: Um motociclista realiza um movimento uniforme e seu espaço varia com o tempo conforme indica o gráfico. Qual é a função horária dos espaços do motociclista?

  

Ex 3: A velocidade escalar de um carro varia com o tempo conforme indica o gráfico.

 a) Determine a aceleração do carro entre os instantes 0 e 10 s e entre 10 e 30 s.

b) Qual é a variação de espaço entre os instantes 0 e 30 s e qual é, neste intervalo, a velocidade escalar média?

Ex 4: O trem do metrô  parte do repouso de uma estação A e realiza um movimento uniformemente variado durante 40 s, atingindo a velocidade de 72 km/h. Mantém esta velocidade por 5 minutos e, a seguir, freia uniformemente e após 20 s atinge a estação B. Qual é a distância, em km, entre as estações A e B? Sugestão: construa o gráfico v x t.

Exercícios de revisão

Ex 1: (UFS-SE) Um carrinho se desloca em trajetória retilínea. O gráfico representa a sua posição s em função do tempo t.

Analise as afirmações sobre o movimento do carrinho.

0 0 - O deslocamento entre os instantes 3,0 s e 8,0 s é de 21 m.
1 1 - A velocidade no instante 12 s é 5,0 m/s.
2 2 - A velocidade média de t = 0 a t = 15 s é 3,5 m/s.
3 3 - A aceleração no instante 7,0 s é nula.
4 4 - A aceleração média no intervalo de 7,0 s a 12 s é 0,60 m/s².

Ex 2: (FATEC-SP) O jipe-robô Curiosity da NASA chegou a Marte, em agosto de 2012, carregando consigo câmaras de alta resolução e um sofisticado laboratório de análises clínicas para uma rotina de testes. Da Terra, uma equipe de testes comandava seus movimentos e lhe enviava as tarefas que deveria realizar. Imagine que, ao verem uma rocha de aspecto muito peculiar, os técnicos da NASA, no desejo de que a Curiosity a analisasse, determinaram uma trajetória reta que une o ponto de observação até a rocha e instruem o robô para iniciar seu deslocamento, que teve duração de uma hora. Nesse intervalo de tempo, o Curiosity desenvolveu as velocidades indicadas no gráfico.

O deslocamento total realizado pelo Curiosity do ponto de observação ao seu destino foi, em metros,

a) 9.         b) 6.         c) 4.         d) 2.         e) 1.


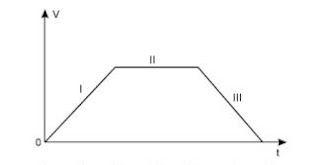
Ex 3: (FGV-SP) Um carro deslocou-se por uma trajetória retilínea e o gráfico qualitativo de sua velocidade (v), em função do tempo (t), está representado na figura.

Analisando o gráfico, conclui-se corretamente que

a) o carro deslocou-se em movimento uniforme nos trechos I e III, permanecendo em repouso no trecho II.
b) o carro deslocou-se em movimento uniformemente variado nos trechos I e III, e em movimento uniforme no trecho II. 
c) o deslocamento do carro ocorreu com aceleração variável nos trechos I e III, permanecendo constante no trecho II.
d) a aceleração do carro aumentou no trecho I, permaneceu constante no trecho II e diminuiu no trecho III.
e) o movimento do carro foi progressivo e acelerado no trecho I, progressivo e uniforme no trecho II, mas foi retrógrado e retardado no trecho III.

Ex 4: (ENEM-MEC) O gráfico abaixo modela a distância percorrida, em km, por uma pessoa em certo período de tempo. A escala de tempo para ser adotada para o eixo das abcissas depende da maneira como essa pessoa se desloca.

Qual é a opção que apresenta a melhor associação entre meio ou forma de locomoção e unidade de tempo, quando são percorridos 10 km?

a) carroça - semana
b) carro - dia
c) caminhada - hora
d) bicicleta - minuto
e) avião - segundo

TRABALHO DE UMA FORÇA CONSTANTE

LISTA DE EXERCÍCIOS SOBRE TRABALHO DE UMA FORÇA CONSTANTE

Exercícios básicos:

Ex 1: Calcule o trabalho da força constante F de intensidade F = 10 N, num deslocamento d = 2,0 m, nos casos indicados abaixo:

Ex 2: Um pequeno bloco de  peso P = 8,0 N, desloca-se numa mesa horizontal passando da posição A para a posição B, sob ação de uma força horizontal F = 10 N. O coeficiente de atrito dinâmico entre o bloco e a mesa é μ_d = 0,50. Determine os trabalhos das forças, F, F_at, P e F_N no deslocamento d = 1,5 m, de A até B.

                                                  

Ex 3: Calcule o trabalho do peso de um bloco de massa 1,0 kg nos deslocamentos de A até B, segundo as trajetórias (1), (2) e (3). Dados: g = 10 m/s² e h = 0,5 m.

Texto referente aos exercícios 4 e 5. 

Uma pequena esfera de peso 1,0 N é lançada obliquamente do ponto A do solo horizontal, com velocidade v0. A altura máxima atingida (ponto B) é h = 2,4 m. O ponto C encontra-se a uma altura h/2 do solo. 

Ex 4: Calcule o trabalho realizado pelo peso da esfera no deslocamento de A até B.


Ex 5:
Calcule o trabalho realizado pelo peso da esfera no deslocamento de B até C.

Exercícios de Revisão

Ex 1: (UFRGS) Um estudante movimenta um bloco homogêneo de massa M, sobre uma superfície horizontal, com forças de mesmo módulo F, conforme representa a figura abaixo.

Em X, o estudante empurra o bloco; em Y, o estudante puxa o bloco; em Z, o estudante empurra o bloco com força paralela ao solo. 
O trabalho realizado pela força aplicada pelo estudante para mover o bloco nas situações apresentadas, por uma mesma distância d, é tal que:

a) W_x = W_y  = W_z 
b) W_x = W_y  < W_z 
c) W_x > W_y  > W_z 
d) W_x > W_y  = W_z 
e) W_x < W_y  < W_z


Ex 2: (ESPECEX) Um bloco, puxado por meio de uma corda inextensível e de massa desprezível, desliza sobre uma superfície horizontal com atrito, descrevendo um movimento retilíneo e uniforme. A corda faz um ângulo de 53° com a horizontal e a tração que ela transmite ao bloco é de 80 N. Se o bloco sofrer um deslocamento de 20 m ao longo da superfície, o trabalho realizado pela tração no bloco será de:
(Dados: sen 53° = 0,8 e cos 53° = 0,6)

a) 480 J
b) 640 J
c) 960 J
d) 1280 J
e) 1600 J

Ex 3: (UERJ) Um objeto é deslocado em um plano sob a ação de uma força de intensidade igual a 5 N, percorrendo em linha reta uma distância igual a 2 m.
Considere a medida do ângulo entre a força e o deslocamento do objeto igual a 15º, e τ  o trabalho realizado por essa força. Uma expressão que pode ser utilizada para o cálculo desse trabalho, em joules, é  τ  = 5 x 2 x sen θ.

Nessa expressão, θ equivale, em graus, a:

a) 15 
b) 30 
c) 45 
d) 75 

Ex 4: (UECE) Em um corredor horizontal, um estudante puxa uma mochila de rodinhas de 6 kg pela haste, que faz 60º com o chão. A força aplicada pelo estudante é a mesma necessária para levantar um peso de 1,5 kg, com velocidade constante. Considerando a aceleração da gravidade igual a 10 m/s², o trabalho, em joule, realizado para puxar a mochila por uma distância de 30 m é 

a) Zero. 
b) 225,0. 
c) 389,7. 
d) 900,0. 


Ex 5: (PUC-RJ) O Cristo Redentor, localizado no Corcovado, encontra-se a 710 m do nível no mar e possui massa igual a 1.140 toneladas. Considerando-se g = 10 m/s², é correto afirmar que o trabalho total realizado para levar todo o material que compõe a estátua até o topo do Corcovado foi de, no mínimo:

a) 00114.000 kJ
b) 00505.875 kJ
c) 1.010.750 kJ
d) 2.023.500 kJ
e) 8.094.000 kJ 

EMPUXO

LISTA DE EXERCÍCIOS SOBRE FORÇA DE EMPUXO

Exercícios básicos

Ex: 1. Um corpo está flutuando em um líquido. Nesse caso

(a) o empuxo é menor que o peso.
(b) o empuxo é maior que o peso.
(c) o empuxo é igual ao peso.
(d) a densidade do corpo é maior que a do líquido.
(e) a densidade do corpo é igual a do líquido

Ex: 2. Uma pedra, cuja a massa específica é de 3,2 g / cm³, ao ser inteiramente submersa em determinado líquido, sofre um perda aparente de peso, igual à metade do peso que ela apresenta fora do líquido. A massa específica desse líquido é, em g / cm³,

(a) 4,8
(b) 3,2
(c) 2,0
(d) 1,6
(e) 1,2

Ex: 3. Um ovo colocado num recipiente com água vai até o fundo, onde fica apoiado, conforme a figura . Adicionando-se sal em várias concentrações, ele assume as posições indicadas nas outras figuras B, C, D e E .

   

A situação que indica um empuxo menor do que o peso do ovo é a da figura

(A) A
(B) B
(C) C
(D) D
(E) E

Ex: 4. Uma esfera maciça e homogênea, de massa específica igual a 2,4 g/cm³, flutua mantendo 20% do seu volume acima da superfície livre de um líquido. A massa específica desse líquido, em g/cm³ , é igual a

(a) 1,9
(b) 2,0
(c) 2,5
(d) 3,0
(e) 12,0

Ex: 5. interior de um recipiente encontra-se um corpo em equilíbrio mergulhado num líquido de densidade 0,8 g/cm³, conforme a figura. Se este mesmo corpo for colocado em outro recipiente, contendo água ( densidade igual a 1g/cm³) podemos afirmar que

(a) o corpo irá afundar e exercer força no fundo do recipiente.
(b) o corpo continuará em equilíbrio, totalmente submerso.
(c) o corpo não flutuará.
(d) o corpo flutuará com mais da metade do volume submerso.
(e) o corpo flutuará com menos da metade do volume submerso

Exercícios de revisão

Ex: 1) Um cubo de borracha de massa 100 g está flutuando em água com 1/3 de seu volume submerso. Sabendo-se que a densidade da água é de 1g/cm3 e tomando-se como aceleração da gravidade g = 10 m/s². Qual é o volume do cubo de borracha?

Ex: 2) Quando um corpo de 3,0 kg está completamente imerso em água, cuja densidade é d = 1,0 g/cm³, apoiado sobre uma balança ela marca 20 N. Calcule o volume desse corpo.

Ex: 3) A figura a seguir mostra uma caixa cúbica de aresta a = 20 cm e massa M = 10 kg, imersa em água, sendo mantida em equilíbrio por um fio muito leve preso ao teto. Determine a tração no fio, em newtons.

Ex: 4) Um bloco de madeira de volume V = 60 cm³, totalmente submerso, está atado ao fundo de um recipiente cheio de água por meio de um fio de massa desprezível. O fio é cortado e o bloco emerge na superfície com 1/4 de seu volume fora da água. Sendo g = 10 m/s² a aceleração da gravidade e D = 1 g/cm³ a massa específica da água, calcule

a) a massa específica do bloco.

b) a tração no fio, antes de ser cortado.

Ex: 5) Um bloco de alumínio, de massa igual a 2,0kg, está pendurado por uma corda de massa desprezível e tem metade do seu volume mergulhado em um recipiente com água. A tensão na corda é igual a 12N. Se acrescentarmos água ao recipiente, de modo que o bloco fique completamente mergulhado, o valor da tensão na corda será (use o valor da aceleração da gravidade, g = 10m/s²):

a) 1 N. b) 2 N. c) 3 N. d) 4 N. e) 5 N.

Ex: 6) Um pedaço de madeira, de densidade 600 kg/m³, possuindo massa de 12000 kg, flutua na água do lago de densidade 1000 kg/m³. Determine o volume da parte emersa desse pedaço de madeira.

Ex: 7) Um copo cilíndrico, vazio, flutua em água, com metade de sua altura submersa, como mostra a fig. 1. Um pequeno objeto, de 1,0N de peso, é posto dentro do copo, com cuidado para que não entre água no copo. Restabelecido o equilíbrio hidrostático, verifica-se que o copo continua a flutuar, mas com 3/4 de sua altura submersos, como mostra a fig. 2.Calcule o peso do copo.

ASSOCIAÇÃO DE RESISTORES II

LISTA DE EXERCÍCIOS SOBRE ASSOCIAÇÃO DE RESISTORES II

Exercícios básicos

Para as associações abaixo (exercícios 1, 2, 3 e 4), calcule a resistência equivalente entre os terminais A e B.

Ex 1:

Ex 2:

sDica: o resistor de 5 Ω, cujos terminais estão ligados por um fio sem resistência está em curto-circuito. Ele pode ser eliminado do circuito.

x

Ex 3:

  

Ex 4:

x

x

Dica: Os pontos A e D, ligados por um fio sem resistência, podem ser considerados coincidentes. O mesmo ocorre com os pontos C e B. Refaça a associação considerando A e D um único ponto, assim como C e B. A seguir, transporte os resistores. Você verá que eles estão ligados em paralelo. 


Ex 5:

Considere o circuito abaixo.

Calcule:

a) as intensidades das correntes i, i₁ e i₂;

b) a potência elétrica dissipada pelo resistor de 8 Ω.

x

Exercícios de revisão

Ex 1: (UFAC) Dois resistores R₁ = R₂ = 600 Ω estão associados conforme a figura:

A resistência equivalente entre os pontos A e B, em ohms, é igual a:

(A) 600 Ω    (B) 1200 Ω    (C) zero    (D) 300 Ω    (E) 400 Ω



Ex 2: (CEFET-AL) Na montagem de um circuito, procede-se conforme a figura abaixo.

A resistência equivalente entre os extremos A e B é igual a:

A) 9,0 Ω
B) 6,0 Ω
C) 3,0 Ω
D) 2,0 Ω
E) 1,0 Ω

Ex 3: (UFPB)

No circuito elétrico representado na figura, os resistores R são iguais e S é uma chave de resistência desprezível.
Sabendo-se que, com a chave aberta, a corrente no circuito é I, com ela fechada será:

a) I/2     b) 2I     c) 4I     d) I/4     e) I

Ex 4: (UFPE) No circuito da figura, a corrente no amperímetro é igual a 3,5 A, quando a chave S está aberta. Desprezando as resistências internas do amperímetro e da bateria, calcule a corrente no amperímetro, em ampères, quando a chave estiver fechada.

A) 4,0
B) 6,0
C) 7,5
D) 8,0
E) 3,5

Ex 5: (UEPG) Observe o trecho de circuito mostrado abaixo: R₁ = 3,0 Ω, R₂ = 6,0 Ω e R₃ = 4,0 Ω. Este trecho de circuito está submetido a uma diferença de potencial ΔV = 18,0 V.
Com relação ao resistor R₁, a corrente elétrica (I₁), a diferença de potencial entre suas extremidades (V₁) e a potência nele dissipada (P₁) é correto afirmar que:

(A) I₁ = 2,0 ampères, V₁ = 6,0 volts e P₁ = 12,0 watts
(B) I₁ = 3,0 ampères, V₁ = 18,0 volts e P₁ = 27,0 watts
(C) I₁ = 3,0 ampères, V₁ = 9,0 volts e P₁ = 27,0 watts
(D) I₁ = 2,0 ampères, V₁ = 9,0 volts e P₁ = 12,0 watts
(E) I₁ = 1,0 ampères, V₁ = 6,0 volts e P₁ = 6,0 watts